Nerves and Towers II: Nerves

An introduction to nerves, one of the fundamental building blocks of TDA.

Nathaniel Saul

3 minute read

The nerve is a simplicial complex built from a cover. It is a discrete summarization of the cover that captures the interesting topological features. Additionally, if the cover is sufficiently refined, then the nerve is guaranteed to preserve the topological features. A nerve of a cover is constructed in a very straight forward way: An (n-1)-dimensional simplex is added for each nonempty n-way intersection of elements of the cover.

The nerve of a cover \(~\mathcal{N}(\mathcal{U})\) is a set of simplices such that $$ \mathcal{N} (\mathcal{U}) = \left\{(j, \ldots, k) : \bigcap_{i = j, \ldots, k} U_i \right\}$$

The one-way intersection of a set is vacuously nonempty, so we add a vertex for every element of the cover. If two sets overlap, then we would add an edge joining the two vertices associated with the sets.

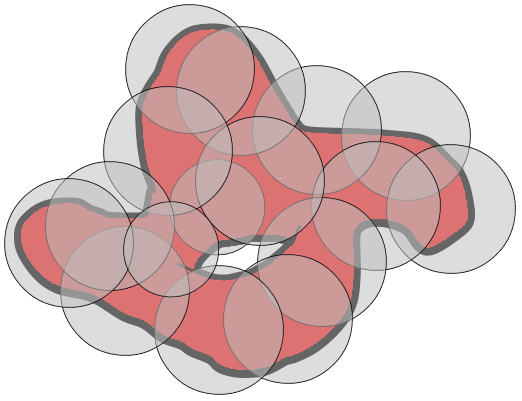
The nerve theorem (as usually stated in texts about mapper, but there are many varieties in different contexts) claim prove strong theoretical guarantees about the topological features of the nerve. In the image above, if the gap in the object was covered, then the resulting nerve would not have a hole, and would not be topologically equivalent to the object. This is what the nerve theorem says.

(Nerve Theorem) Given a cover \(~\mathcal{U}\) of \(~X\), if each intersection of elements of the cover is contractible and our original space is compact, then the nerve of \(~\mathcal{U}\) is weakly equivalent to \(~X\).

Unfortunately, we cannot apply the theorem to most settings in TDA, so instead we use ideas of persistence to estimate the topological features.

The mapper is one of the main objects from Topological Data Analysis. It a construction that lets you view data using a function as the lens. This is useful because often modern data is extremely high dimensional. The function allows users to map the data into considerably lower dimensional space, use this information to build a nerve, and then visualize the high dimensional structure as a graph. It puts together all the definitions we have built so far.

Given a function \(~f: X \to Y\) and a cover \(~\mathcal{U}\) of \(~Y\), the mapper is defined as \(~\mathcal{N}(f^* (U))\).

In short, we choose an \(f\) from our data to a much lower dimensional space (one that has some intuitive meaning to us, say height, or net worth), we then create a cover of this low dimensional space, find the pullback cover, and then build the nerve of the pullback cover.

For an introduction to mapper that appeals more to intuition rather than theory, check out this other post I wrote.

,