In unsupervised learning, one of the main questions we want to answer is what type of structure does this set or shape have? The field of algebraic topology supplies a few tools to help answer this question. We can ask topological questions about the data, such as how many clusters or connected components are there? or are there gaps, holes, or voids in the data?. These question can be easy to answer if the shape is well defined, but in practice, we instead have data sampled from that shape. If we can construct a representation of the underlying shape, maybe we can estimate these properties instead. These questions and methods to answer them are central to the field of Topological Data Analysis (TDA).

The nerve is a simplicial complex constructed from overlapping sets and is fundamental to many techniques of TDA. Given a sufficiently good cover of a space, the nerve of that cover is topologically equivalent to the underlying space. This gives us a way to represent the essential properties of a space through a much condensed lens.

The two main methods from TDA, persistent homology and mapper, both use the nerve in their construction. Persistent homology computes the nerve of growing balls around the data points and instead of using the nerve thoerem to prove correctness, it looks at the most persistent features to say which are most probable to be features instead of noise. Mapper computes the nerve of the pullback cover of some function, creating a simplicial complex representation of the data with respect to a function of interest, say the height or distance from the origin. Leveraging the idea of towers, mapper can be extended to a multiscale mapper so that tools from persistence theory can also be applied.

In this series of posts, we will build up the necessary definitions and theorems to understand multiscale mapper. We will lay the groundwork for understanding nerves and towers, and introduce the basic ideas of the multiscale mapper.

• Part I: Basics
• Part II: Nerves
• Part III: Towers

We will introduce some basic concepts typically found in an undergraduate analysis or topology class. For all definitions to come, let \(X\) be some topological space, maybe the object depicted below.

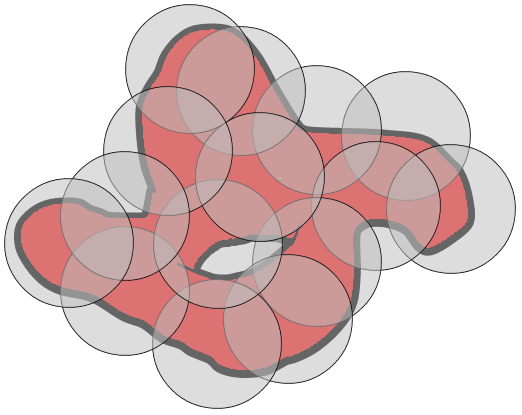
A cover of \( X \) is a set of subsets of \(X\) that completely covers \(X\). This is a way to group the elements of a set into smaller, more manageable subsets and string them all together.

Cover is a particularly descriptive name. Feel free to think of a cover as a set of blankets, all together, completely covering the set, and probably containing some overlap. If the object is small enough, only one blanket is needed, if it is big, we might have lots of partially overlapping blankets. The important part is that there is no part of the set that is not covered by at least one blanket and there could be overlap between the blankets.

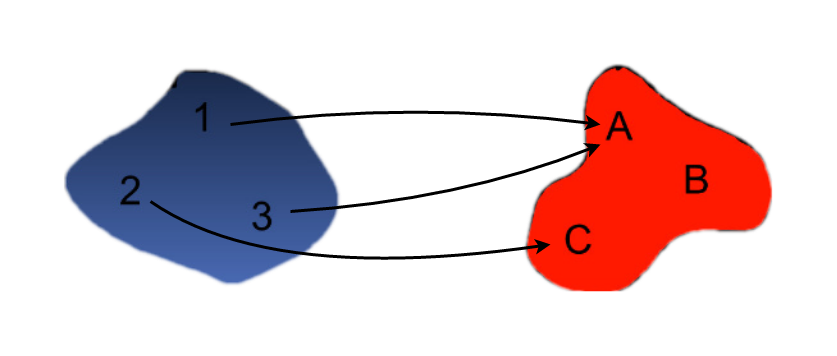
A pullback cover of a function gives us a way to build a cover of the domain of a function through a cover of the codomain.

It could be helpful to visualize the pullback cover on a trivial example. Suppose we have a function \(f: \{1,2,3\} \to \{A, B, C\}\) defined as

$$ f(1) = A \ f(2) = A \ f(3) = C $$

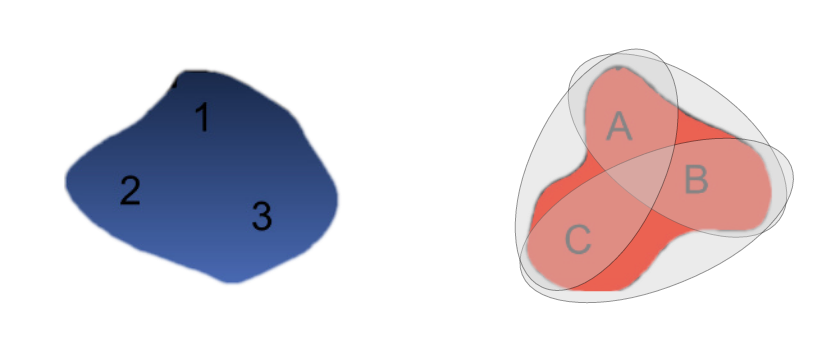
We can then define a cover of \(\{A, B, C\}\) as all pairs of items:

$$\mathcal{U} = { {A,B}, {B,C}, {C,A} }$$

Clearly the union of these three sets is our original set.

We can then pull this cover back through \(f\) by finding the preimage of each element of the cover. We get the resulting pullback cover to be \(f^* (\mathcal{U}) = \{ \{1,2,3\}, \{1,3\}, \{2\} \}\).

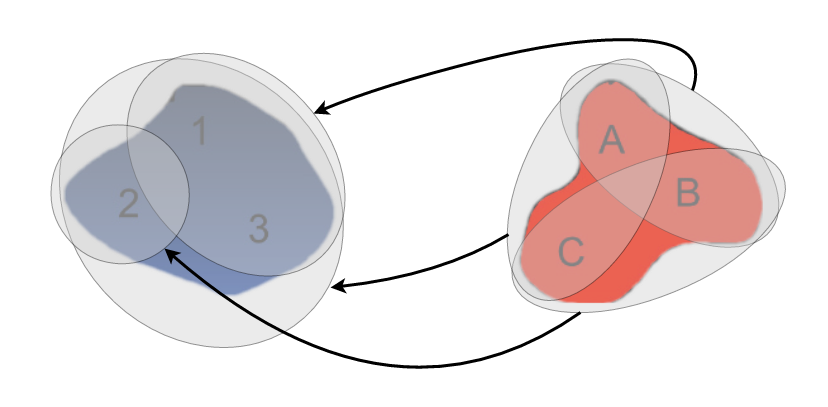
In the next post we will make use of these definitions by introducing the nerve and mapper.

• Part II: Nerves