Nerves and Towers III: Towers

An introduction to towers, an extension of mapper to the world of persistence.

Nathaniel Saul

6 minute read

Once we understand the tower, we will show that it plays nice with all of the other definitions we have constructed so far and how it allows us to naturally define a multiscale mapper.

A tower \(~\mathcal{T} \) is a tuple ( \(T_\epsilon\), \(\{t_{\epsilon, \epsilon^\prime}\}\)) of indexed objects \( T_\epsilon \) with morphisms \[t_{\epsilon, \epsilon^\prime}: T_\epsilon \to T_{\epsilon^\prime} \] defined when \( \epsilon \le \epsilon^\prime \). Additionally, we must have that morphisms are composable, that is \( t_{\epsilon, \epsilon^\prime} \circ t_{\epsilon^\prime, \epsilon^{\prime \prime}} = t_{\epsilon, \epsilon^{\prime \prime}} \). The resolution of \( \mathcal{T} \), \( r = res(\mathcal{T})\) if \( r \le \epsilon \) for all \(T_\epsilon\).

An example of a tower is a partially ordered set (poset) where each morphism represents inclusion. For a trivial example, say \(X = \{a,b,c\}\), then we could create a tower with \(T_3 = X\), \(T_2 = \{a,b\}\), and \(T_1 = \{a\}\). We can then define inclusions \(T_1 \subset T_2 \subset T_3\), with \(T_1 \subset T_3\).

How can we construct a tower of covers. A tower of sets with inclusion doesn’t necessary have to consist of distinct layers, where each layer is a cover. We could instead be much more general, where each subset is an element and the morphisms are inclusion.

We will define a tower of covers based on inclusion maps.

Example: Tower of covers
Let (Ti) objects of the tower, each one a cover of (X). Then for (j>i), we define a map (t{i,j}: T_i \to T_j) if each element of (T_i) is subset of an element of (T_j).

To ensure that this map is well defined, we must set extra conditions of the covers \(T_i\). Specifically, for each element \(\tau \in T_i\), there must be no other \(\gamma \in T_i\) such that \(\tau \subset \gamma\). This ensures that any \(\tau \in T_i\) could only be mapped to one element of \(Tj\) and thus \(t{i,j}\) will be well defined. The composition of these maps holds, \(t{i,j} \circ t{j,k} = t_{i,k}\). These requirements force a sort of telescoping structure on our tower of covers.

A pullback of tower of covers is also a tower of covers.

We will define two different tower of covers that can be constructed in practice.

Example: Splitting tower
Begin with a single element cover of (X). Progressively split each element of the cover in half. Discard an (\mathcal{O}_i) where (\mathcal{O}_i \bigcap X = \emptyset). Continuing for (n) iterations, we have (res (\mathcal{T}) = diam(X)/n).

For ease of visualization, the images below will show the towers of two disjoint intervals.

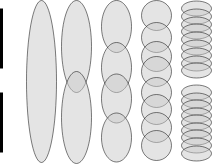
After a certain point of splitting, there are elements of the cover that don’t contain any elements, these can be discarded.

Example: Shrinking tower
Begin with a cover of \(X\) with \(n\) elements each with no overlap. Then for each layer, increase the size of each element until each element individually covers \(X\). We can then use the same inclusion maps.

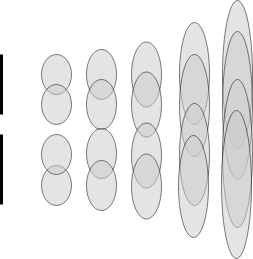
Note that in the picture above, the inclusion morphisms would go from right to left, i.e., the tower is upside down.

Given a tower of covers \(\mathcal{T}\), we can construct a tower of simplicial complexes by taking the nerve of each element of the cover and considering the simplicial maps induced from the inclusion maps. We will show that the induced simplicial maps do indeed create a tower.

Given simplicial complexes \(K\) and \(L\), A mapping $$ f: K \to L $$ is a simplicial map if for each simplex \(\sigma \in K\), \(f(\sigma)\) is a simplex in \(L\).

These maps are completely determined by their behavior on the vertices. A simplicial map can be decomposed into inclusions and vertex collapses. That is, for simplicial map \(f: K \to L$, a simplex is either mapped directly into the image, or two vertices are mapped to the same vertex and the associated simplices follow directly.

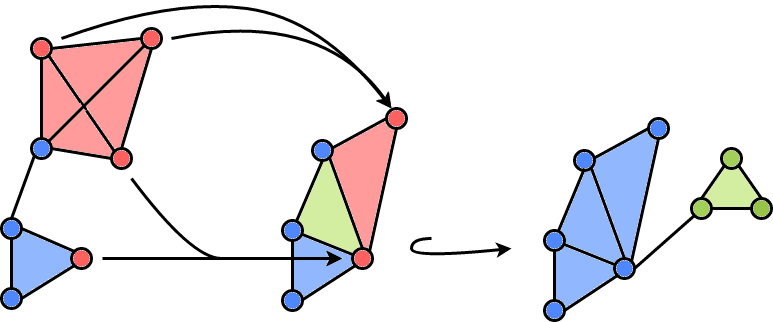
The image above shows three simplicial complexes connected by simplicial maps. The blue simplicies are included, the red simplices share a preimage, and the green simplices are in the cokernal of the maps (no simplices map to these simplices). A filtration is a tower where each simplicial map is an inclusion, i.e. the sequence of complexes are nested.

The nerve of a tower of covers is a tower of simplicial complexes.

We can then define the multiscale mapper as the nerve of the pullback of a tower of covers. Multiscale mapper is a tower analog of the mapper construction introduced by Dey et al in 2015. By considering a tower of covers and constructing the mapper at each layer of this tower, we can construct a tower of simplicial complexes with simplicial maps.

The multiscale mapper is found by computing the nerve of each cover of a tower of covers. $$ \mathcal{N}(f^* (\mathcal{T}))$$ It is a tower of simplicial complexes.

Using techniques developed by Dey et al in 2012, we can convert this tower of simplicial complexes into a filtration. The persistent homology of the multiscale mapper can then be computed using classic methods. Checkout Sophia for a way to compute persistence on towers.

References

,